基于二项分布检验法的水质达标评价方法研究

　1 引言

　　水质达标评价(Water Quality Compliance Assessment)是根据一定时段内的水质监测数据，评价水体状态是否符合其功能对应的水质标准的决策过程，是流域水污染防治和水质管理的重要科学依据.区别于水质评价研究中对水质综合指标、时间序列趋势、季节性特征等的关注，水质达标评价的关注点是水质是否达标，并可以由此评估已有的流域治理措施效果、制定新的治理规划(如TMDL).在流域水污染防治资金紧缺的条件下，准确识别水体是否达标至关重要：如果评价方法过于保守，会导致水生态系统健康受损;若评价方法过于严格，会导致水体过于保护，水体自净能力无法得到有效利用及高的治理资金投入.科学合理的水质达标评价方法是进行水质达标评价的基础.我国地表水环境质量评价采用单因子评价方法，对断面时空监测数据求算术平均值判断其水质类别，根据断面水质类别比例对流域水质进行分级.美国清洁水法303(d)条款规定对受损水体实施TMDL计划，EPA导则推荐使用监测数据的90%分位数评价水体是否受损，即监测数据的超标个数不能超过10%.在欧盟，采用每年12个月监测数据的算术平均值作为评价依据，少数成员国将监测数据的变异性考虑在内，给出统计置信区间.

　　水质指标监测值存在不确定性已经被广泛地认识和研究.我国水质达标评价方法未考虑水质指标的不确定性，美国和欧盟已经将不确定性纳入到水质达标评价中.水质指标的不确定性包括固有的变异性(如监测数据的季节性差异)和可减小的不确定性(如测量误差)2部分.通过合理选择监测断面、监测指标以及质量保证和质量控制(QA/QC)可以减小不确定性，却不能完全消除.忽视不确定性可能会带来巨大的决策风险，科学合理的水质达标评价方法必须能够表征监测数据的不确定性，将由水质指标不确定性带来的决策风险定量化，为决策提供有用信息.

　　在统计学视角下，将水质指标视为随机变量，可有效地表征不确定性.水质指标具有时空分异性，在同一时间获得空间所有点位的监测数据或者在同一点位进行连续的监测是不可能的，只能通过有限的监测数据对水质进行评价，即根据样本数据估计总体特征.统计学假设检验方法已经广泛应用于环境系统中，假设检验的2类错误可以定量表征水质指标的不确定性带来的决策风险.针对美国EPA提出的最大超标率为10%，Smith等和McBride等认为10%应该指10%的时间，即总体分布的90%分位数，并采用二项分布检验法(Binomial Test)进行了水质达标评价.该方法是一种针对二元数据的非参数方法，通过假设检验给出在一定允许超标率和样本容量时的最大超标个数，并与实际监测得到的超标个数对比，评价水质是否超标.尽管研究者指出二项分布检验法存在信息损失的问题，并提出了参数检验方法，然而McBride的研究表明，在大部分情况下，二项分布检验法由于不受限于原始数据的分布而更具有鲁棒性.本文以基于二项分布检验法的水质达标评价方法为基础，分析其决策过程及决策风险的定量表征，并以海河流域为例，对比不同评价方法的差异性，分析其适用性和灵活性.

　　2 研究方法

　　2.1 基于二项分布检验法的水质达标评价方法

　　在二项分布检验法之前，需将监测数据转化为0~1变量，方法为：对于某一特定监测数据x，将其与水质标准θ对比，对比后的结果记为y，如果x>θ，即超过水质标准，记y=1;如果x≤θ，记y=0.令p(0<p<1)为成功概率，表示x>θ的概率，则y服从成功概率为p的0~1分布，其分布律为：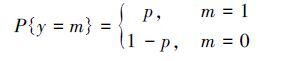

(1)

　　假设收集到的N个监测数据用于评价水质是否达标，记随机变量X=x1，x2，...，xN，将X中的每个元素转化为0~1变量，便得到随机变量Y=y1，y2，...，yN，则Y服从参数为(N，p)的二项分布，记为Y~B(N，p).令n为Y成功的总次数，即为N个样品中超标总个数，其分布律为：

(2)

　　二项分布的分布律表征了水质变量转化为二元数据后超标总个数不确定性.欲检验总体分布的90%分位数是否达标，即超标率是否小于10%，可令原假设为水质达标，即H0:p≤0.1，备择假设为H1:p>0.1.原假设为真时，可得p=0.1时超标个数n的分布函数F;实际监测数据中超标个数nc不应太大，在给定的显著性水平α下，应有F(nc)=P(n≤nc)≤1-α;否则拒绝原假设，判定为水质超标.

　　2.2 弃真错误和取伪错误

　　在经典统计学的假设检验过程中，不可避免地要讨论2类错误：弃真错误和取伪错误.在水质达标评价中，这2类错误是由于水质变量的不确定性导致的.弃真错误为当原假设为真时，放弃原假设而犯的错误(falsely inferring a breach of standard)，弃真错误的概率记为α;取伪错误为当原假设为假时，相信原假设而犯的错误(falsely inferring compliance)，弃伪错误的概率记为β.对于二项分布，$\alpha =P\left( n>{{n}_{s}} \right)=\sum\limits_{j={{n}_{s}}+1}^{N}{C_{N}^{j}{{P}^{j}}}{{\left( 1-P \right)}^{N-j}}$.计算β时，需要给定效应值η(备择假设和原假设之间的差距)，二项分布检验法一般取η=0.15，即p′=p+η=0.25来计算β，计算公式为β=G-1(ns)，其中G(n)=$\sum\limits_{k=1}^{N}{C_{N}^{k}{{P}^{'k}}}{{\left( 1-P' \right)}^{N-k}}$，为成功概率为p′的二项分布的分布函数，G-1(n)为G(n)的反函数.

　　按照上述α和β的计算公式，可以得到N一定时，以不同的ns(0≤ns≤N)作为决策准则(即nc>ns判定为超标，nc≤ns判定为达标)时，α和β的变化情况.由图 1可知N一定时，对于特定的ns存在唯一的(α，β)组合;α随ns减小，β随ns增加.图中竖直虚线假设变量服从对称分布，算术平均值等于50%分位数，则平均值法等价于最大允许超标率为50%.图中竖直实线代表采用10%超标样品数目(以下称为“超标比例法”)得到的ns，当N=12时，ns=1，α=0.341;当N=50时，ns=5，α=0.384.可见对于相同样本容量，平均值法弃伪错误的概率很大，超标比例法弃真错误的概率较大，而二项分布检验法则可根据决策者需要选择不同的(α，β)组合.相对于选择特定的显著性水平值做决策，(α，β)组合能量化决策准则的风险，为决策者提供更大的决策空间.α和β随N增加均有减小的总体趋势，参见Smith等.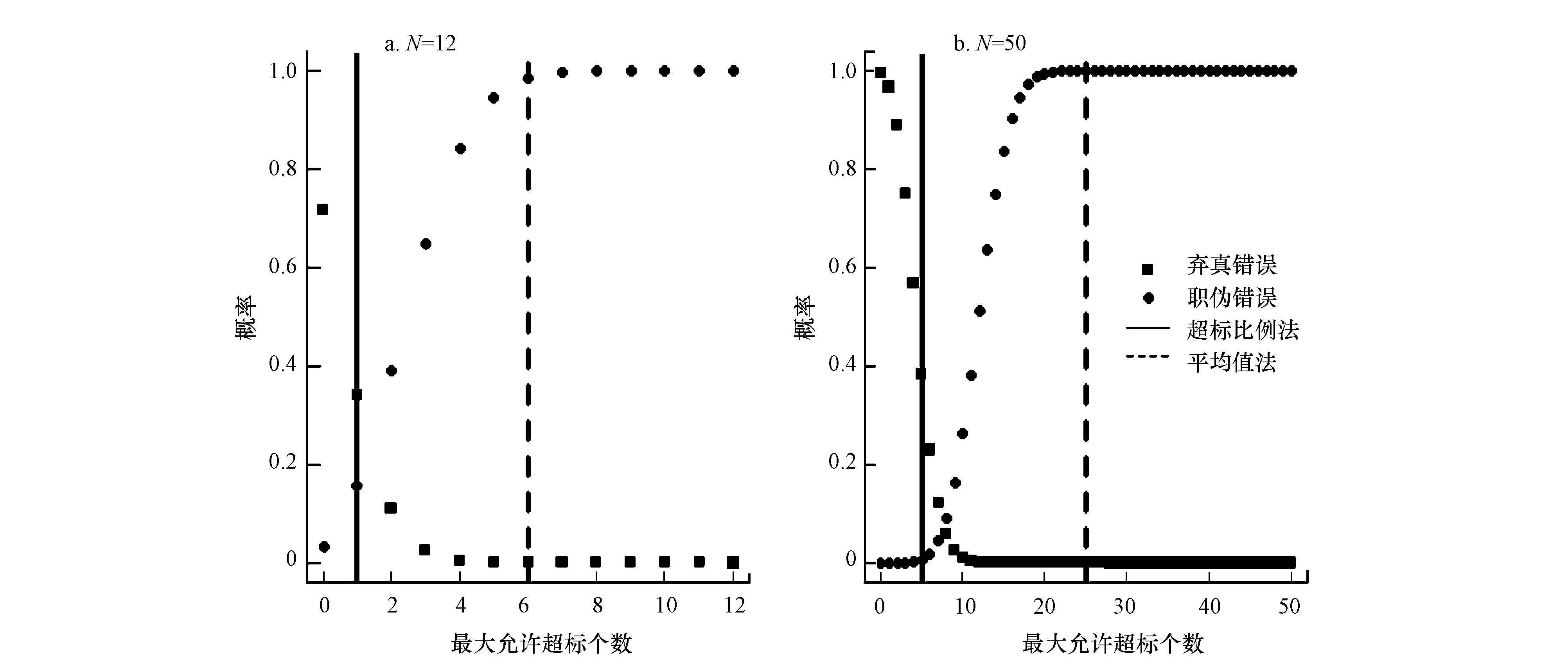

　　图 1N=12(a)和50(b)时2类错误概率随最大允许超标个数的变化

　　2.3 决策过程

　　基于二项分布检验法的水质达标评价的决策过程包括2个环节：首先确定ns，然后根据监测样品的超标个数nc判断水质是否达标.一般而言，决策过程应该使得α和β最小.在N一定时，由于α、β随ns单调性相反(图 1)，对于特定的ns不能同时使α和β最小.作为决策者，在选择ns时：一方面，需要根据风险偏好和科学判断，选择最大允许超标率p;另一方面，需要权衡各相关方的利益，如：作为受体人群和生态系统的及作为治理投资者的政府或企业.在同等条件下，ns随着p的增大而不严格单调递增;在p和N一定时，根据决策者的利益权衡，可以得到不同的ns.

　　下面介绍3种典型的(α，β)组合选择策略：①保证α在一定的低水平，例如α≤0.05，使得β最小;②保证β在一定的低水平，例如β≤0.05，使得α最小;③控制α≈β，即minα-β.图 2给出了当p=0.1，N为4~100时，这3种策略得到的最大允许超标个数ns和最大允许超标率η=nsN(散点图，连续线为点过于密集的结果).可见当N较小时，控制α≤0.05得到的ns最大，控制β≤0.05得到的ns最小，且当N≤10时，无论如何选择ns均不能使β≤0.05;随着N变大，控制α≤0.05得到的ns最小，控制β≤0.05得到的ns最大;策略③的结果介于①和②之间.总体上，控制α≤0.05得到的η呈递减趋势，由于假设检验是p=0.1时二项分布的95%分位数，因此η恒大于0.1(图 2d虚线);控制β≤0.05得到的η呈递增趋势，由于假设检验是p=0.25时二项分布的5%分位数，因此η恒小于0.25(图 2e虚线).综上，基于二项分布检验法的水质达标评价决策过程可表示为图 3.决策者可以根据风险偏好和利益权衡，选择p值和(α，β)组合，进而确定N一定时的ns，结合水质监测数据中的实际超标个数nc，对水体的达标状况进行判断;通过p和(α，β)可将决策的各种风险定量化.

　　图 2(Fig. 2)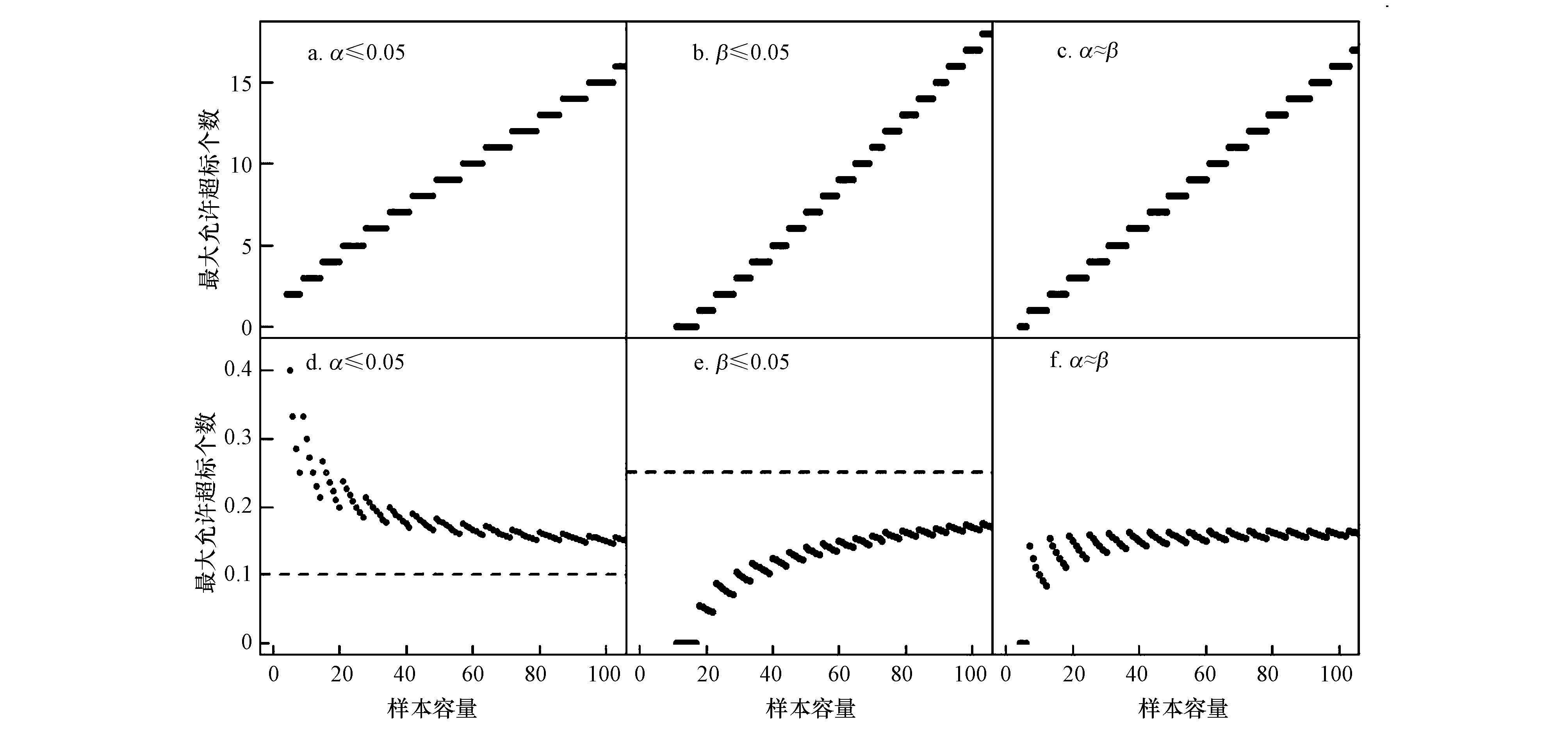

　　图 2最大允许超标个数和最大允许超标率随样本容量的变化

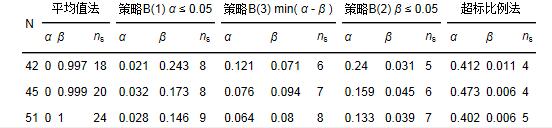
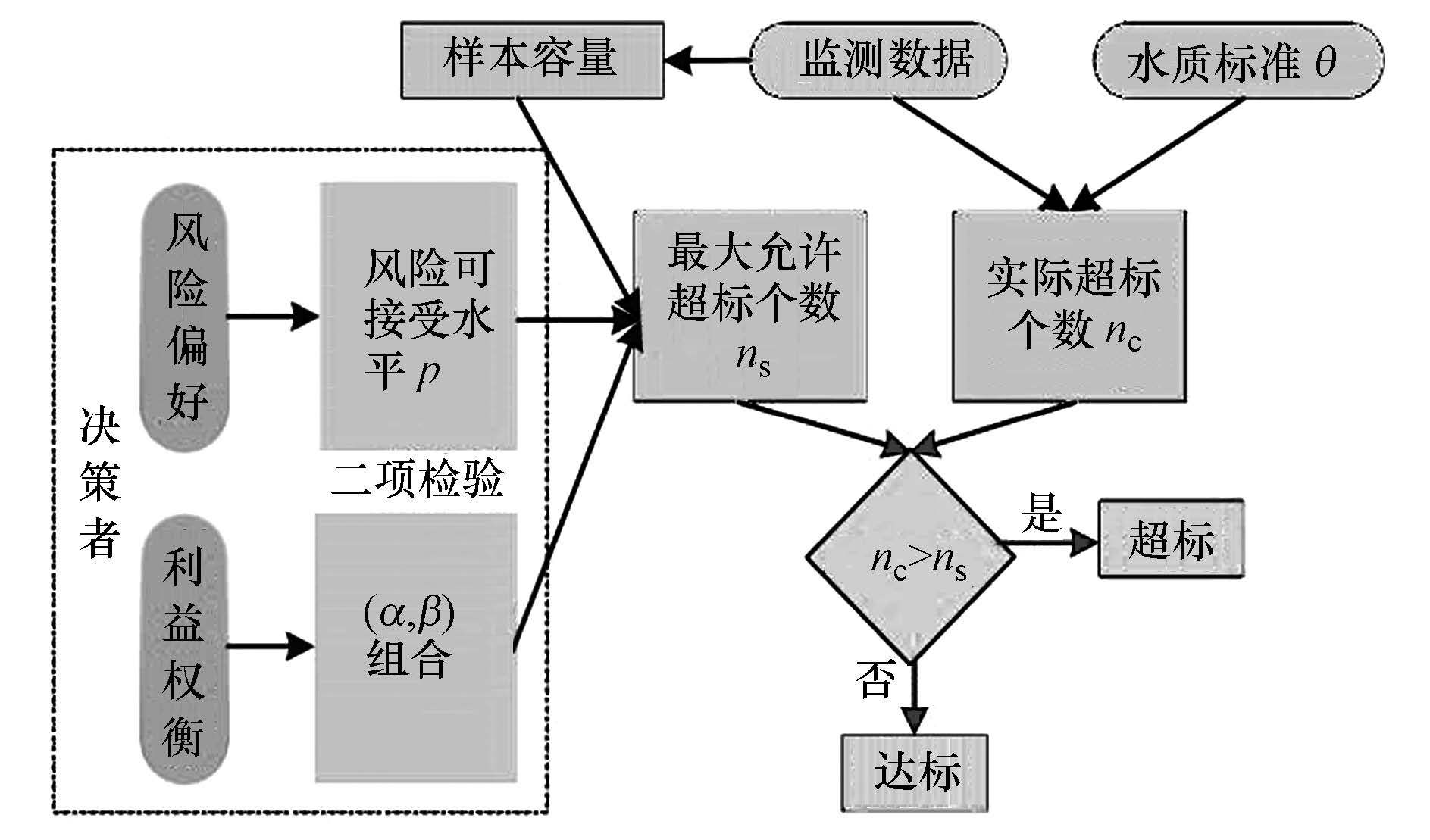　　图 3基于二项分布检验法的水质达标评价决策过程

　　3 案例研究(Case study)3.1 研究对象和方法

　　选择海河流域的CODMn作为达标评价的对象，数据来源为环保部网站，收集2014年7月22日-2015年7月14日的周监测数据，共有北京密云古北口(51)、北京门头沟沿河城(51)、天津三岔口(51)、天津果河桥(51)、河北张家口八号桥(45)、河北石家庄岗南水库(51)、山东聊城秤钩湾(42)等7个监测断面，括号中为不同监测断面的有效监测样品数.

　　当N=42、45、51时，采用平均值法、二项分布检验法的3种策略、超标比例法确定α、β、ns(对于平均值法，求各个样本中大于平均值的样品个数，作为平均值法的ns)，对比监测数据与地表水环境质量标准中各水质类别的浓度限值θi(i=1，2，...，5)，得到超过θi的样品个数nci，水质类别判定遵循如下过程：当i=1时，若nc1≤ns则水质类别判定为I类;当i=5时，若nc5>ns则判定为劣V类;若nci≤ns<nc(i-1)则判定为i类.最后，根据地表水环境质量评价办法(试行)对流域水质进行分级.本文的所有统计方法和运算均在r软件(version:r-3.2.3，https: p="" )中实现.<="" www.r-project.org="">

　　3.2 水质评价结果

　　各种方法对应的α、β、ns结果见表 1，各种方法的严格程度为：超标比例法>B(2)>B(3)>B(1)>平均值法(“a>b”表示a严格于b，B(i)表示二项分布检验法的第i种策略);采用平均值法β接近于1，超标比例法得到的α很大(>0.4)，二项分布检验法的3种策略得到的2类错误之和小于0.3，平均在0.2左右，且均处于相对较低水平.水质评价结果见表 2，在7个断面中，石家庄岗南水库水质最好，聊城秤钩湾水质最差;石家庄岗南水库和门头沟沿河城2个断面采用各种方法的评价结果相同，另外5个断面有差异.根据断面的水质类别得到的流域分级结果也有差异.断面水质类别的评价结果，除了与评价方法的严格程度有关，也与水质监测数据有关.采用相对严格方法评价达标的断面，在不严格方法下自然达标;采用相对不严格方法评价达标的断面，在严格的方法下不一定达标，例如密云古北口采用平均值法评价为I类水质，而采用其它方法评价时却为II类水质.总体上看，评价结果符合严格方法得到的水质类别较低的规律.

　　表 1 3种样本容量对应的各种评价方法的2类错误概率和最大允许超标个数

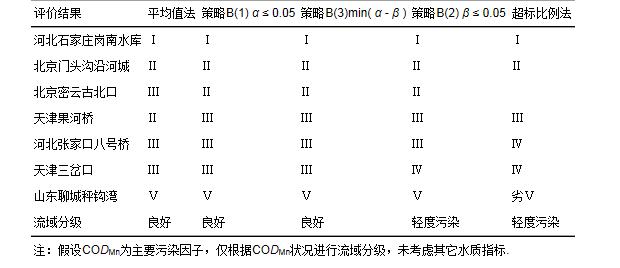
　　表 2 海河流域CODMn达标评价结果

　　综合表 1和表 2，对于二项分布检验法的3种方法，控制β≤0.05有利于保护受体的利益，对水体水质要求严格，流域分级为“轻度污染”;控制α≤0.05有利于减少治理投资，对流域分级为“良好”;二项检验的3种策略的评价结果对比，说明在采用二项分布检验法进行水质达标评价时，即使对于完全相同的水质监测数据，决策时倾向于不同利益群体，可能得出不同的水质达标评价结果.二项分布检验法为水质达标评价的决策提供了较为广阔的决策空间.

　　案例研究中，取最大超标率p=0.1，采用二项分布检验法的3种典型策略进行水质达标评价;在实践中，决策过程有更大的灵活性：对于p，决策者可以根据风险偏好选择不同值.对于策略①和②，决策可设定不同的错误概率限值，例如令α≤0.1使得β最小，再比如，可同时限定α，β的最大值，例如令α≤0.2同时β≤0.1，即可得到多组(α，β)组合;对于策略③，可根据需要设定限制条件，例如出于保护受体的目的令α<β，或者给定最大可接受的差值δ，令α-β≤δ，亦可得到不同的(α，β)组合.对得到的多组(α，β)组合，决策者可结合其它约束条件进行优选确定最终的ns.

　　4 讨论

　　4.1 先验知识与假设检验

　　研究中采用的原假设是水质达标，α代表水质达标而判定为不达标的概率，β代表水质未达标而判定为达标的概率，二项分布检验法的策略①实质上是求成功概率为p的二项分布的95%分位数;Gibbons指出如果有很强的先验知识认为水体超标，则假设检验的原假设应为水质未达标，此时α和β的含义互换，而二项分布检验法的策略①变为求成功概率为p的二项分布的5%分位数.由计算可得，当先验知识认为水质超标时，得到的ns较小.如当效应值为0.15，样本容量N=50，最大超标率p=0.25时，按策略①，原假设为水质达标时ns=18，原假设为水质超标时ns=7，则对于超标个数在8~18的样本按照2种原假设得到的评价结果不同，例如当nc=10时，若原假设为水质达标，则判定为达标，若原假设为水质超标，则判定为超标.可见，水质现状的先验知识对评价结果具有显著影响，在先验知识充足时，水质达标评价具有“宽进严出”的规律，即将先验认为达标的水体列为不达标状态时对超标个数的要求较为保守，而将先验认为未达标水体列为达标状态时对超标个数的要求较为严格.β值与效应值的选取有关，本文参照文献做法取效应值为0.15，即备择假设的p=0.25.在同等条件下，尽管根据不同效应值可以得到不同的β，但是其随N和ns的变化规律一致.假设检验的效果随样本容量的增加而增大，对海河流域的研究显示，采用二项分布检验法可以控制各个断面的总错误概率平均值在0.2左右，评价结果具有很高的可信度.

　　4.2 最大允许超标概率的选择

　　对于研究中最大超标率设定的目的，研究者给出了不同的解释：Smith等、McBride等认为水质变量不确定性造成的某次监测数据超标是难以避免的，因此对全部水质监测数据给出一个可以接受的超标率(10%)是合理的;此时10%可理解为“容忍度”.Gibbons则认为对90%分位数进行假设检验是为了保证总体的均值小于标准值;此时，样本均值与90%分位数之间的差异可理解为“安全因子”.Smith等针对的是一类分位数标准(percentile-based standards)，而Gibbons针对的则是平均值标准，平均值代表流域水质变量波动性的平均水平，与室内实验或野外试验的稳定浓度相对应.本文建议，在使用二项分布检验法进行水质达标评价时，需要首先区分评价变量的标准类型，如果是分位数标准，则根据要求选择较小的p值(例如0.1)是合理的;如果是平均值标准，过大的安全因子会导致水质目标难以实现，需要选择较大的p值(例如0.25).

　　结合4.1和4.2小节，最大允许超标概率和假设检验的2类错误率均是由于水质监测数据的不确定性导致的.最大允许超标概率体现了由于监测数据波动性，而对其采用的“容忍度”或者“安全因子”，决策者对最大允许超标概率的选择体现了风险偏好;假设检验的2类错误体现了由于水质变量的不确定性，使用样本估计总体特征的可信程度，决策者对2类错误的选择体现了对不同群体的利益权衡.通过这3个参数，基于二项分布检验法的水质达标评价方法将水质监测数据的不确定性对决策过程的影响定量化，对决策的各种风险进行了定量表征，使得决策更具科学性.

　　5 结论

　　1) 水质变量存在不确定性，平均值法忽视了水质变量的不确定性，会造成很大的取伪错误概率，而超标比例法会导致很大的弃真错误概率;基于二项分布检验法的水质达标评价方法可以将由水质变量的不确定性导致的决策风险定量化，为决策者提供科学依据.

　　2) 本文在基于二项检验的水质达标评价方法的基础上，纳入决策者的风险偏好和对利益的权衡，提出了水质达标评价的决策框架.二项分布检验法对原始数据的分布没有要求，是一种方便快捷的非参数方法.本文提出的决策框架，可为决策者提供较大的决策空间，决策者可以根据风险偏好和利益权衡选择或限制最大超标率、效应值、弃真错误概率和取伪错误概率组合，确定最大允许超标个数，进行水质达标评价.

　　3) 对海河流域的水质评价结果表明，采用基于二项分布检验法的水质达标评价方法，相对于平均值法和超标比例法，其评价结果具有很高的可信度，不同的利益权衡会得到不同的评价结果，验证了二项分布检验法的适用性和灵活性.